861. Суммирование матрицы
Матрица n × n заполнена числами. BuggyD анализирует матрицу и хочет найти сумму
некоторых подматриц, то есть он хочет записать результаты своих запросов.
Матрица динамическая, значение в любой ячейке может быть изменено.
В начале все
ячейки матрицы заполнены 0. Разработайте программу для BuggyD.
Вход. Первая строка содержит количество тестов t.
Первая строка каждого теста содержит одно целое число n (1 ≤ n ≤ 1024) – размер матрицы.
Далее следует набор команд в одном из трех форматов:
"SET x y num"
– установить значение ячейки (x, y) равной num (0 ≤ x, y < n).
"SUM x1
y1 x2 y2"
– найти сумму чисел в прямоугольнике от (x1,
y1) до (x2, y2) включительно. Считайте, что x1 ≤ x2
и y1 ≤ y2, результат помещается в
знаковое 64-битное целое.
"END" - указывает на конец теста.
Выход. Для каждого
запроса "SUM" выведите в отдельной строке ответ на него. после
каждого теста выводите пустую строку.
|
Пример
входа |
Пример
выхода |
|
1 4 SET 0 0 1 SUM 0 0 3 3 SET 2 2 12 SUM 2 2 2 2 SUM 2 2 3 3 SUM 0 0 2 2 END |
1 12 12 13 |
РЕШЕНИЕ
структуры
данных – дерево Фенвика двумерное
Анализ алгоритма
Пусть mat – текущая
матрица. Построим для нее двумерное дерево Фенвика t. Пусть sum(x, y) – это функция, которая находит сумму
чисел на прямоугольнике (0, 0) – (x,
y) при помощи дерева Фенвика за время O(![]() ). Тогда сумма чисел на прямоугольнике (x1, y1) – (x2,
y2) равна
). Тогда сумма чисел на прямоугольнике (x1, y1) – (x2,
y2) равна
sum(x2, y2)
– sum(x1
– 1, y2) – sum(x2, y1 – 1) + sum(x1 – 1, y1 – 1)
Присвоение mat[x][y] = num
эквивалентно прибавлению к mat[x][y] значения num – mat[x][y] (дерево Фенвика реализует только
операцию прибавления на отрезке, а не присваивание).
Реализация алгоритма
Пусть mat –
текущая матрица, t – двумерное дерево Фенвика (дерево сумм для матрицы mat).
vector<vector<int> > t, mat;
Сумма на прямоугольнике (0, 0) – (x, y).
int sum(int
x, int y)
{
int result =
0;
for (int i = x; i >= 0; i = (i & (i + 1)) - 1)
for (int j = y; j >= 0; j = (j & (j + 1)) - 1)
result += t[i][j];
return
result;
}
Прибавление элемента: mat[x][y] += delta.
void add(int
x, int y, int
delta)
{
for (int i = x; i < n; i = (i | (i+1)))
for (int j = y; j < n; j = (j | (j+1)))
t[i][j] += delta;
}
Основная часть программы. Читаем входные данные. Обнуляем
матрицы.
scanf("%d",&tests);
while(tests--)
{
scanf("%d",&n);
t.assign(n+1,vector<int>(n+1,0));
mat.assign(n+1,vector<int>(n+1,0));
while(scanf("%s ",s),strcmp(s,"END"))
{
if (s[1] ==
'E') // set
{
Обработка команды SET. Присвоение mat[x][y] = num промоделируем через прибавление:
mat[x][y] += num – mat[x][y]
(дерево Фенвика реализует только
операцию прибавления на отрезке).
scanf("%d
%d %d",&x,&y,&num);
if
(mat[x][y] != num)
{
add(x,y,num - mat[x][y]);
mat[x][y] = num;
}
} else // sum
{
Обработка команды SUM.
scanf("%d
%d %d %d",&x1,&y1,&x2,&y2);
res = sum(x2,y2) - sum(x1-1,y2) -
sum(x2,y1-1) + sum(x1-1,y1-1);
printf("%d\n",res);
}
}
После каждого теста выводим пустую строку.
printf("\n");
}
Реализация алгоритма – двумерное дерево отрезков
Рассмотрим
двумерную матрицу m размером 4 * 4. Пусть изначально все ее ячейки равны нулю. Отобразим
дерево отрезков для интервала [0; 3]. Возле каждой его вершины укажем индекс
ячейки массива, в которой она будет находиться.
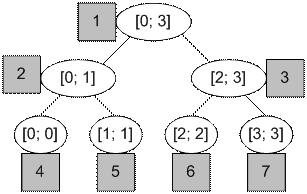
Двумерное дерево
отрезков для моделирования запросов на массиве m будет иметь вид квадратной матрицы SegTree размера 8 * 8 (нулевая
строка и столбец не используются).
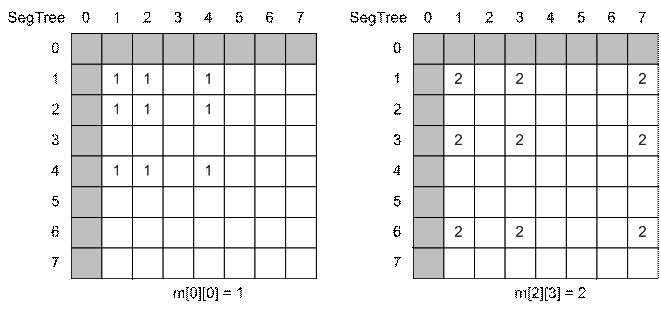
Совершим два
присваивания одновременно. Получим следующее состояние дерева отрезков:
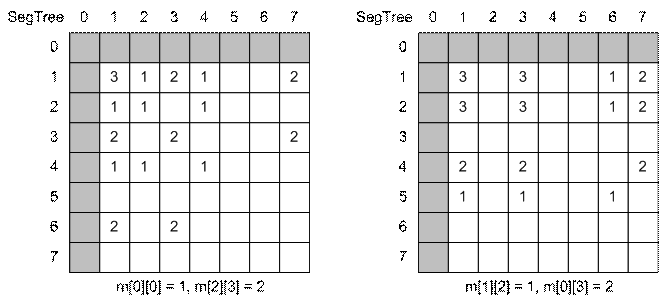
#include <stdio.h>
#include <string.h>
#define MAX 1030
int SegTree[4*MAX][4*MAX];
int n, tests;
char s[10];
int x, y, x1, y1, x2, y2, num, res;
int min(int
x, int y)
{
return (x
< y) ? x : y;
}
int max(int
x, int y)
{
return (x
> y) ? x : y;
}
void sety(int
xVertex, int xLeftPos, int
xRightPos, int yVertex,
int yLeftPos, int yRightPos, int
yPos, int NewValue)
{
if (yLeftPos
== yRightPos)
{
if
(xLeftPos == xRightPos)
SegTree[xVertex][yVertex] = NewValue;
else
SegTree[xVertex][yVertex] =
SegTree[2*xVertex][yVertex] + SegTree[2*xVertex+1][yVertex];
}
else
{
int Middle
= (yLeftPos + yRightPos) / 2;
if (yPos
<= Middle)
sety(xVertex, xLeftPos,
xRightPos, 2*yVertex, yLeftPos, Middle,
yPos,
NewValue);
else
sety(xVertex, xLeftPos,
xRightPos, 2*yVertex+1, Middle+1,
yRightPos, yPos, NewValue);
SegTree[xVertex][yVertex] =
SegTree[xVertex][2*yVertex] + SegTree[xVertex][2*yVertex+1];
}
}
void set(int
Vertex, int LeftPos, int
RightPos,
int xPos, int yPos, int
NewValue)
{
if (LeftPos
!= RightPos)
{
int Middle
= (LeftPos + RightPos) / 2;
if (xPos
<= Middle)
set(2*Vertex, LeftPos, Middle, xPos,
yPos, NewValue);
else
set(2*Vertex+1, Middle+1, RightPos, xPos,
yPos, NewValue);
}
sety(Vertex,LeftPos,RightPos,1,0,n-1,yPos,NewValue);
}
int gety(int
yVertex, int LeftPos, int
RightPos, int xVertex,
int yLeft, int yRight)
{
if (yLeft
> yRight) return 0;
if ((yLeft ==
LeftPos) && (yRight == RightPos))
return
SegTree[xVertex][yVertex];
int Middle =
(LeftPos + RightPos) / 2;
return
gety(2*yVertex, LeftPos, Middle,
xVertex, yLeft, min(yRight,Middle)) +
gety(2*yVertex+1, Middle+1,
RightPos, xVertex,
max(yLeft,Middle+1), yRight);
}
int get(int
Vertex, int LeftPos, int
RightPos,
int xLeft, int yLeft, int
xRight, int yRight)
{
if (xLeft
> xRight) return 0;
if ((xLeft ==
LeftPos) && (xRight == RightPos))
return
gety(1,0,n-1,Vertex,yLeft,yRight);
int Middle =
(LeftPos + RightPos) / 2;
return
get(2*Vertex, LeftPos, Middle,
xLeft, yLeft, min(xRight,Middle), yRight) +
get(2*Vertex+1, Middle+1, RightPos,
max(xLeft,Middle+1),
yLeft, xRight, yRight);
}
int main (void)
{
scanf("%d",&tests);
while(tests--)
{
memset(SegTree,0,sizeof(SegTree));
scanf("%d",&n);
while(scanf("%s ",s),strcmp(s,"END"))
{
if
(!strcmp(s,"SET")) // set
{
scanf("%d
%d %d",&x,&y,&num);
set(1,0,n-1,x,y,num);
} else // sum
{
scanf("%d
%d %d %d",&x1,&y1,&x2,&y2);
res = get(1,0,n-1,x1,y1,x2,y2);
printf("%d\n",res);
}
}
printf("\n");
}
return 0;
}